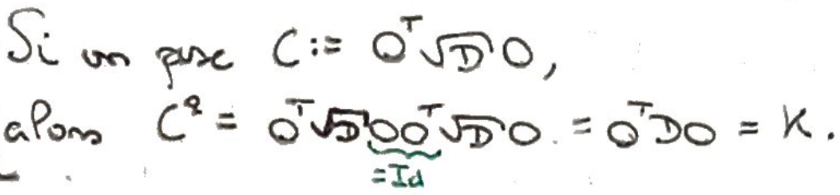Matrice symétrique définie positive

Formulaire de report

Problème d'affichage Contenu de la note peu pertinent

• si l'inégalité est large et non stricte, on dira que \(M\) est symétrique positive
• cela revient à dire que l'Endomorphisme \(u\) associé à \(M\) est symétrique
  défini positif
• caractérisation pour les matrices réelles : (critère de Sylvester) : les Mineurs principaux de \(M\) sont tous \(\gt 0\)
• on a la décomposition unique \(M=O^TDO\), avec \(O\) orthogonale et \(D=\begin{pmatrix}\lambda_1&&0\\ &\ddots\\ 0&&\lambda_d\end{pmatrix}\)

Questions de cours

Montrer que toute matrice symétrique définie positive est le carré d'une matrice symétrique positive.

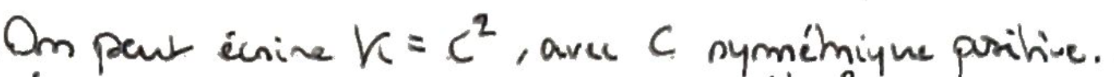
On a la décomposition de diagonalisation.

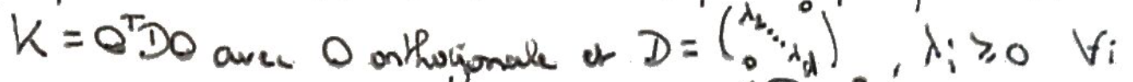
\(D\) est diagonale, donc on peut facilement trouver une racine carrée.

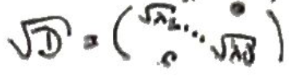
Remplacer \(D\) par \(\sqrt D\) dans la décomposition fonctionnne \(\to\) le vérifier.